3. A Geometric Proof
Proof: Angle HEG has measure theta
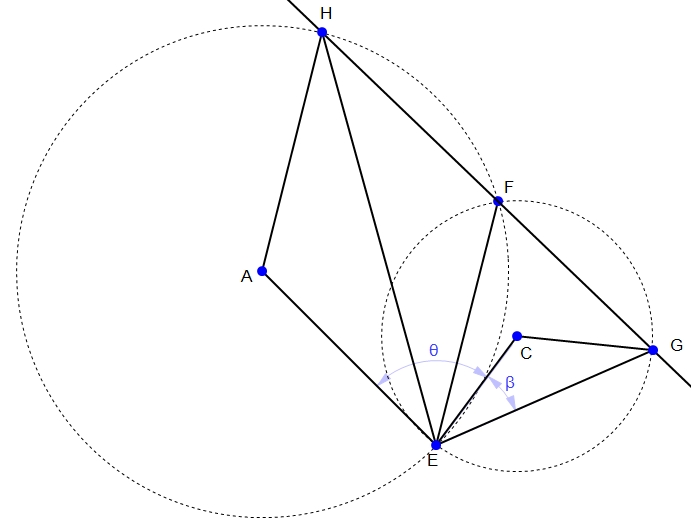
Figure 1—The Base Figure:
Here we have two circles whose center points are A and C and whose intersection points are E and F. Points G and H are on circles C and A respectively. We have constrained line HG to go through point F and angles AEC and CEG are constrained as theta and beta. Our objective is to prove that angle HEG is always theta also when the above conditions are met.
Geometry Expressions Proof:
Draw the figure with all of the above constraints. Calculate angle HEG. If the output is theta, then (assuming Geometry Expressions is correct) we have proven that the angle is theta. This video goes through the proof with Geometry Expressions:
Interactive Version
Formal/traditional Proof:
To prove that angle HEG is theta, first prove that angle AEH is beta. To do this, we show that triangles HAE and GCE are isosceles because two of their sides are radii and the third is a chord. Therefore, angle CGE is also beta and angle ECG is pi-(2*beta) because of the triangle angle sum theorem. Then, the chord angle theorem tells us the value of angle EFG. In this case, angle EFG is (pi/2)-beta. Additionally, because GFH is a line, angle EFH is (pi/2)+beta.
Figure 2: circle C angles
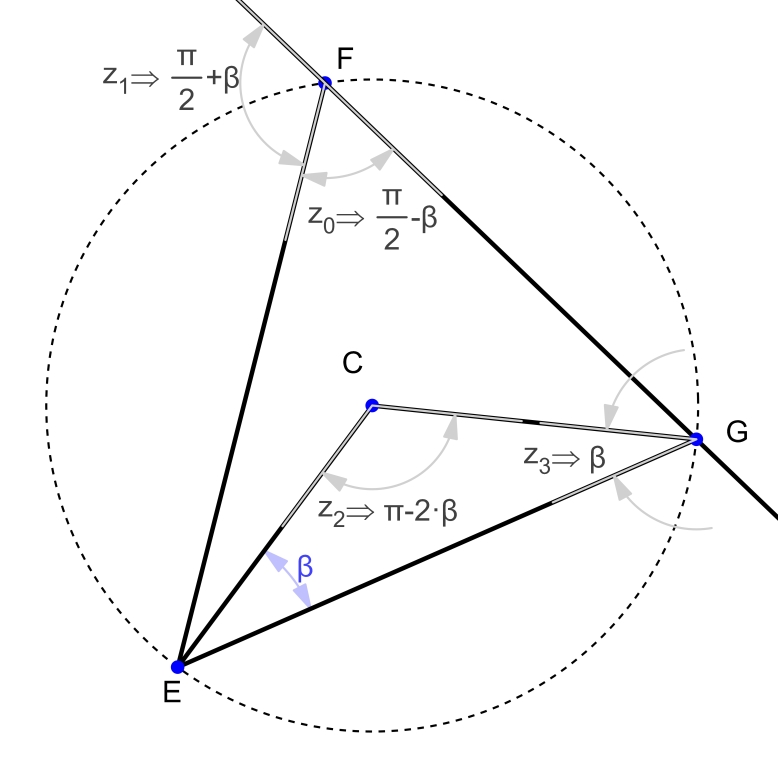
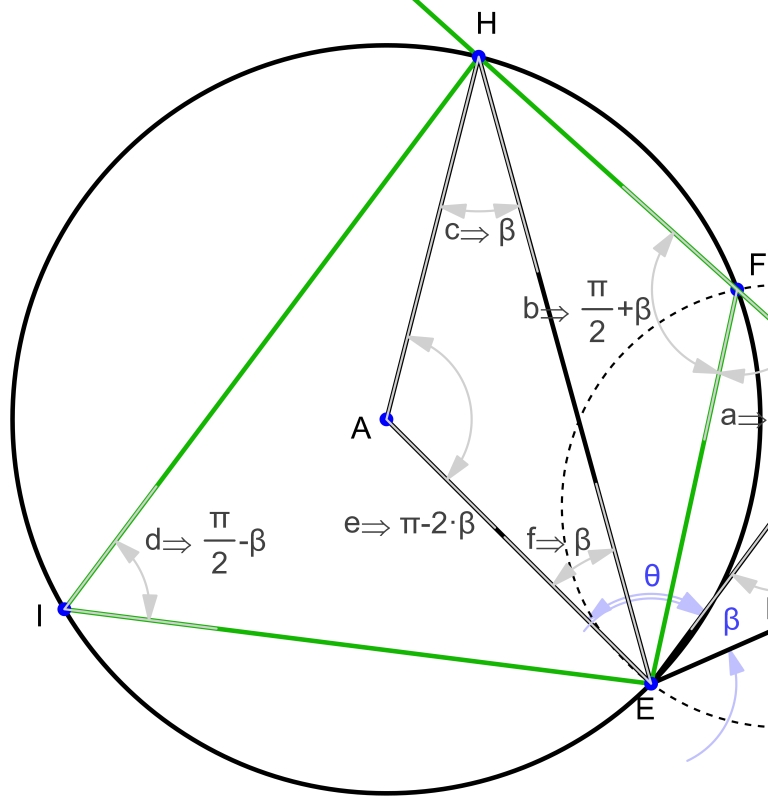
Using the cyclic quadrilateral theorem, we know angle HIE from angle HFE. Then we again use the chord angle theorem to find angle HAE. Because the triangle is isosceles, we have proven that angle AEH is beta (figure 3). Finally, we know through the addition of angles AEC and CEG that angle AEG is equal to beta+theta and that angle AEH is beta, so angle HEG must be theta to satisfy that angle AEG is beta+theta (figure 4).
Figure 3—circle A angles:
Figure 4—final figure:

| Previous | Next |