8. Finding the Surface Area Limit

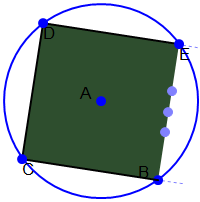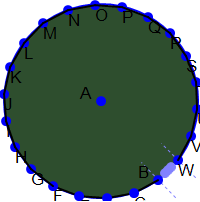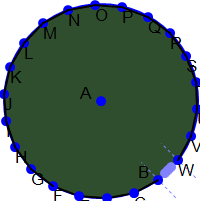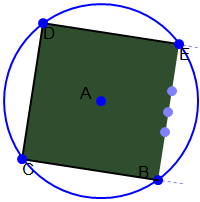
Regular polygons approximating a circle, as the approximation models approximate the turbine

Triangle approximation models were created using 4, 6, 8, 10, 12, 14, 16, 18, 20, 24, 28, and 32 sides. These represented regular polygons of two times the appromations’ number of sides approximating the shape of a circle. For example, the four sided approximation uses an octagon to approximate a circle. The more sides in the model, the closer the calculated surface area will be to the actual surcafe are of the blade. Unfortunately, the symbolic formula for the surface area—in terms of the twist angle theta—could not be calculated due to the formula’s (possibly infinite) length. Therefore, it was determined that the approximate area calculations for each model could be used to see how each model with more and more sides approached the surface area limit. The parameters a, r, and theta of each of the approximation models were set to the same values and the resultant area calculations were graphed as the dependent variable, with the number of sides being the independent variable. The slope of the line connecting each of these points was calculated and shows how the derivative (rate of change) is approaching zero; thus, the graph is approaching a limit:

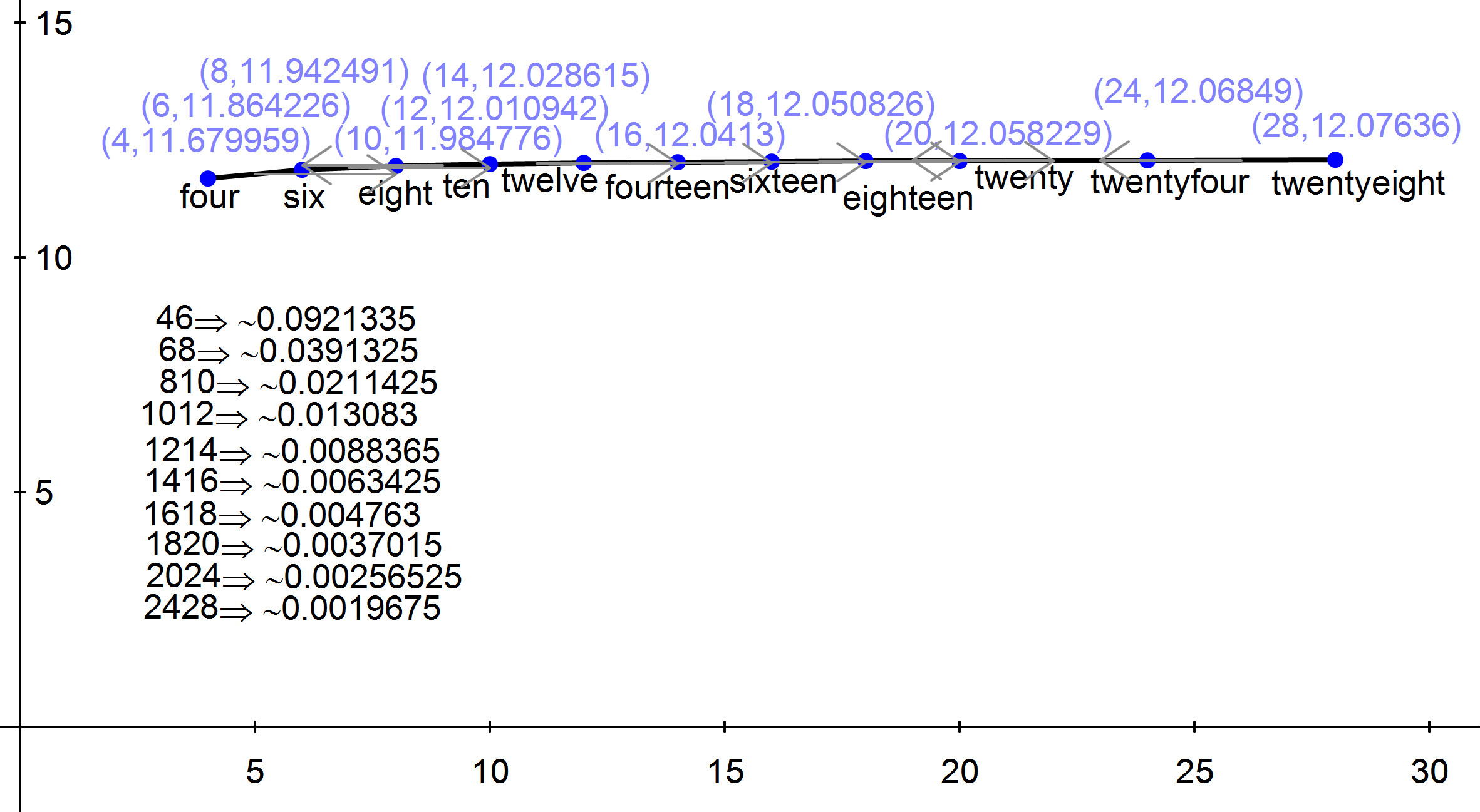
When the 32 side approximation is added to this graph, the slope is within about .001, so the 32 side approximation can be determined close enough to the limit to be used to determine the surface area of the actual blade This likely also means that a scaled-up version of the 32 side approximation could be used in place of the actual turbine shape for an operational turbine design. To learn more about the applications of the model, click here. To see all of the cutout approximation models, click here.